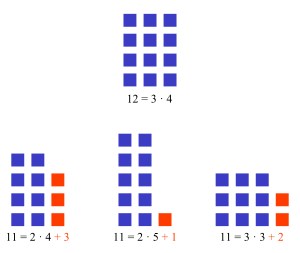Prothsche Primzahl

Prothsche Primzahlen sind natürliche Zahlen, die sowohl Proth-Zahlen als auch Primzahlen sind. Sie sind benannt nach François Proth (1852–1879).
Unter Proth-Zahlen versteht man hierbei natürliche Zahlen der Form ${\displaystyle \ k\cdot 2^{n}\, 1\ }$, wobei ${\displaystyle k}$ und ${\displaystyle n}$ positive natürliche Zahlen sind und ${\displaystyle k}$ eine ungerade Zahl ist, welche zugleich kleiner als die Potenz ${\displaystyle 2^{n}}$ ist.

Die kleinsten Proth-Zahlen sind 3, 5, 9, 13, 17, 25, 33 und 41.
Prothsche Primzahlen davon sind 3, 5, 13, 17 und 41, keine Primzahlen und damit zusammengesetzte Proth-Zahlen dagegen 9, 25 und 33.

Wissenswertes

Jede ungerade Zahl und damit jede Primzahl größer als 2 lässt sich eindeutig in der Form ${\displaystyle k\cdot 2^{n} 1}$ schreiben. Ist eine solche Zahl eine Primzahl und gilt zusätzlich ${\displaystyle k<2^{n}\ }$, so handelt es sich um eine Prothsche Primzahl.

Die Bedeutung der Prothschen Primzahlen liegt darin, dass François Proth einen einfachen Test gefunden hat (Satz von Proth), mit dem sich nachweisen lässt, ob Proth-Zahlen Primzahlen sind. Viele der derzeit größten bekannten Primzahlen wurden mit diesem Test gefunden und es gibt ein frei verfügbares Programm von Yves Gallot, das den Satz von Proth implementiert und häufig für solche Zwecke benutzt wird.

Der Satz von Proth besagt:

Die Proth-Zahl ${\displaystyle N}$ ist prim, falls es eine natürliche Zahl ${\displaystyle a}$ gibt mit:

${\displaystyle a^{\frac {N-1}{2}}\equiv -1\ {\pmod {N}}}$

Die Prothschen Primzahlen spielen auch bei den Sierpiński-Zahlen insofern eine Rolle, als eine Folge von Zahlen der Form ${\displaystyle k\cdot 2^{n} 1\ }$ frei von Prothschen Primzahlen sein muss, damit ${\displaystyle k\ }$ eine Sierpiński-Zahl sein kann.

Unter den Prothschen Primzahlen befinden sich auch Cullen-Primzahlen (C₁ = 3, C₁₄₁ = ${\displaystyle 141\cdot 2^{141} 1}$, ...). Das sind Primzahlen der Form ${\displaystyle k\cdot 2^{k} 1}$.

In der folgenden Tabelle finden sich Primzahlen nach ${\displaystyle k}$ geordnet bis 10.000.000. Primzahlen mit ${\displaystyle k>2^{n}\ }$, die also keine Prothschen Primzahlen sind, stehen in Klammern. Prothsche Primzahlen mit ${\displaystyle k=1}$ nennt man auch Fermatsche Primzahlen.

Die ersten Proth-Zahlen bis 500 lauten:

3, 5, 9, 13, 17, 25, 33, 41, 49, 57, 65, 81, 97, 113, 129, 145, 161, 177, 193, 209, 225, 241, 257, 289, 321, 353, 385, 417, 449, 481, … (Folge A080075 in OEIS)

Die ersten Proth-Primzahlen bis 1000 lauten:

3, 5, 13, 17, 41, 97, 113, 193, 241, 257, 353, 449, 577, 641, 673, 769, 929, … (Folge A080076 in OEIS)

Beispiele

Beispiel 1: (Prothsche Primzahl)

Sei ${\displaystyle k:=3}$ und ${\displaystyle n:=2.}$ Dann ist ${\displaystyle N=k\cdot 2^{n} 1=3\cdot 2^{2} 1=13}$ eine Proth-Zahl, weil ${\displaystyle k=3}$ ungerade und ${\displaystyle 3=k<2^{n}=2^{2}=4}$ ist.

${\displaystyle N=13}$ ist eine Prothsche Primzahl, wenn eine natürliche Zahl ${\displaystyle a\in \mathbb {N} }$ existiert, sodass ${\displaystyle a^{\frac {N-1}{2}}=a^{\frac {13-1}{2}}=a^{6}\equiv -1{\pmod {13}}}$ gilt. Man probiert also alle Zahlen durch, bis man ein geeignetes ${\displaystyle a}$ findet:

${\displaystyle {\begin{aligned}1^{\frac {13-1}{2}}&=&1^{6}&=&1&&&\equiv &1{\pmod {13}}\\2^{\frac {13-1}{2}}&=&2^{6}&=&64&=&5\cdot 13-1&\equiv &-1{\pmod {13}}\end{aligned}}}$

Somit hat man gleich am Anfang schon ein geeignetes ${\displaystyle a=2}$ gefunden, das den Beweis erbringt, dass ${\displaystyle N=13}$ eine Prothsche Primzahl ist. Auch ${\displaystyle a=5,6,7,8,11}$ sind geeignete Zahlen für diesen Beweis.

Beispiel 2: (Primzahl, aber keine Prothsche Primzahl)

Sei ${\displaystyle k:=3}$ und ${\displaystyle n:=1.}$ Dann ist ${\displaystyle N=k\cdot 2^{n} 1=3\cdot 2^{1} 1=7}$ keine Proth-Zahl, weil ${\displaystyle k=3}$ zwar ungerade, aber ${\displaystyle 3=k\not <2^{n}=2^{1}=2}$ ist. Allerdings ist ${\displaystyle N=7}$ eine Primzahl, aber eben keine Prothsche Primzahl.

Beispiel 3: (keine Primzahl)

Sei ${\displaystyle k:=5}$ und ${\displaystyle n:=4.}$ Dann ist ${\displaystyle N=k\cdot 2^{n} 1=5\cdot 2^{4} 1=81}$ eine Proth-Zahl, weil ${\displaystyle k=5}$ ungerade und ${\displaystyle 5=k<2^{n}=2^{4}=16}$ ist.

${\displaystyle N=81}$ ist eine Prothsche Primzahl, wenn eine natürliche Zahl ${\displaystyle a\in \mathbb {N} }$ existiert, sodass ${\displaystyle a^{\frac {N-1}{2}}=a^{\frac {81-1}{2}}=a^{40}\equiv -1{\pmod {81}}}$ gilt. Man probiert also wieder alle Zahlen durch, bis man ein geeignetes ${\displaystyle a}$ findet:

${\displaystyle {\begin{aligned}1^{\frac {81-1}{2}}&=&1^{40}&=&1&\equiv \ &1{\pmod {81}}\\2^{\frac {81-1}{2}}&=&2^{40}&=&1.099.511.627.776&\equiv \ &70{\pmod {81}}\\3^{\frac {81-1}{2}}&=&3^{40}&=&&\equiv \ &0{\pmod {81}}\\4^{\frac {81-1}{2}}&=&4^{40}&=&&\equiv \ &40{\pmod {81}}\\5^{\frac {81-1}{2}}&=&5^{40}&=&&\equiv \ &4{\pmod {81}}\end{aligned}}}$

Analog findet man auch bei allen anderen ${\displaystyle a}$ kein geeignetes, das die Bedingung ${\displaystyle a^{\frac {81-1}{2}}\equiv -1{\pmod {81}}}$ erfüllt. Natürlich gibt es Rechenregeln für die Modulorechnungen, sodass man hohe Zahlen umgehen kann.

Somit hat man den Beweis erbracht, dass ${\displaystyle N=81}$ keine Prothsche Primzahl ist (was eigentlich von vornherein klar war, da ${\displaystyle N=3\cdot 3\cdot 3\cdot 3}$ ist).

Größte bekannte Proth-Primzahlen

Die drei größten derzeit bekannten Proth-Primzahlen sind:

Literatur

• Hans Riesel: Prime Numbers and Computer Methods for Factorization. Reprint of the 1994 Edition (= Progress in Mathematics. Band 126). Birkhäuser, Boston 2017, ISBN 978-0-8176-8297-2 (MR1292250). 

Weblinks

• Eric W. Weisstein: Proth Prime. In: MathWorld (englisch).
• Yves Gallot's Proth.exe: an implementation of Proth's Theorem for Windows – Programm von Yves Gallot
• Proth Search Page
• Chris Caldwell: Proth prime auf The Prime Pages
• List of primes k · 2ⁿ 1 for k < 300
• List of primes k · 2ⁿ 1 for 300 < k < 600
• Startseite des Internet-Projektes “Seventeen or Bust”
• Proth prime. In: PlanetMath. (englisch)

Anmerkungen

Einzelnachweise